Fractals are self-similar objects, that is, they appear the same at different scales. First theorized in the 17th century by the mathematician and philosopher Gottfried Leibniz, fractal shapes are common in the empirical world, with examples including plants, coastlines, human blood vessels and pulmonary vessels, DNA, and ocean waves.

The Mandelbrot Set is the most popular, the most studied, and the most fascinating mathematical fractal discovered by humanity. This gift of Natures takes its name from the mathematician Benoit Mandelbrot, notorious for his monumental contribution to the field of fractal geometry. A subset of the Complex plane defined by the properties of the simple polynomial $z^2 + c$, it contains an infinite amount of astonishingly beautiful and incredibly complex patterns.

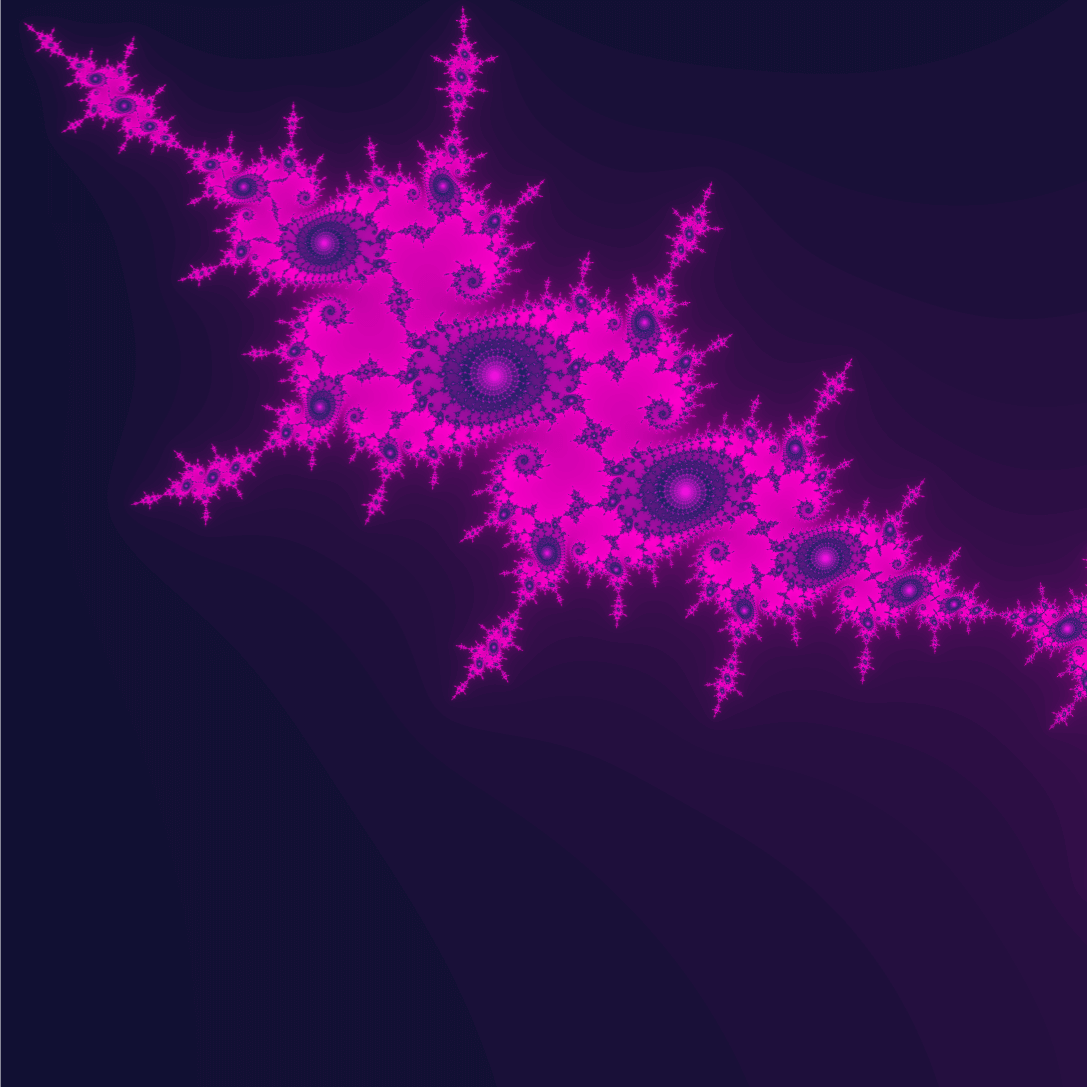
Even though exploring the totality of its richness is impossible for finite beings, we are fortunate enough to live in the age of information. Modern computers allow us to numerically approximate the boundaries of the Mandelbrot set up to a certain level of depth. However, the magic world hidden in the Mandelbrot becomes more complex and more interesting as one increases the zoom factor. As our civilization advances and more powerful computing machines will become available, future generations will have the luxury of enjoying the deeper and deeper wonders of the Mandelbrot.

Mathematically, the Mandelbrot is defined as the set of points $c$ of the complex plane for which the function $ f(z) = z^2 + c $ does not diverge to infinity when iterated from $z=0$. Here $c$ and $z = a + b\,i $ are complex numbers with real and imaginary components, and $z^2 = a^2 - b^2 + 2ab\,i$ denotes the complex product of $z$ with itself.

The Mandelbrot Set Collection is a curated selection of points from the Mandelbrot, generated with a numerical algorithm and engraved into 1978 unique NFTs. Each work represents the neighborhood of one of our favorite points of the fractal, with a random zoom factor and colored with arbitrary gradients based on the number of iterations of $f$ before the point diverges to infinity.

Not all the attributes are equally likely, thus giving rise to different degrees of scarcity for each artwork. In particular, higher zoom levels are limited and golden-colored points are very scarce. Attribution is random, so we wish you the best of luck in unveiling one of the most out-of-the-ordinary pieces.

To learn more about fractals and the Mandelbrot set, look at the following references: